PAGE NSI PREMIÈRE. GABIN ROUMEGUERE
Projet du Chapitre1:Notation Pix
Convertir en note sur 20 un score pix.
Le programme sera à créer sur python. Nous allons utiliser une formule pour calculer la note: note=a*score+b
La note moyenne sera choisie par l'utilisateur. Il faudra donc calculer le score moyen en établissant une fonction moyenne, puis, trouver le score maximal et le score minimal. Enfin, en plus, il faudra aller chercher les prénoms des élèves et leurs scores dans un document, puis, afficher un graphique montrant les différentes notes.
Calcul de a et de b.
Pour trouver la note, il faut trouver les deux constantes, a et b:

Comment trouver le maximum et le minimum dans une liste
Il y a plusieurs méthodes pour calculer le maximum et le minimum d'une liste. Personnellement, j'ai utilisé une méthode trouvée sur le site:https://www.delftstack.com/fr/howto/python/python-max-value-in-list/
Pour les calculer et montrer le fonctionnement du programme, je vais en créer un pour montrer comment calculer le maximum:
Pour trouver le minimum, il suffit de remplacer dans la structure conditionnelle > par <.
Pour expliquer les différentes valeurs temporaires, en premier, la variable max_value va prendre 55, puis grâce à la structure conditionelle if, max_value va changer si il y a eu une valeur plus grande qu'elle dans la liste.


Calcul du score moyen
Pour faire la moyenne des scores, il faut additionner l'ensemble des scores et diviser cette somme par le nombre de score, en python, on va obtenir la somme avec la fonction sum() qui va additionner l'ensemble des valeurs de la liste et le diviseur avec la fonction len() qui va donner le nombre de valeurs d'une liste. On a donc le programme suivant, avec une boucle for() qui va s'appliquer sur la liste numbers.


Sortir des infos d'un document
Pour sortir les infos d'un document, M.Laclaverie nous a donné un programme que j'ai moi même appliqué dans le projet pour sortir le nom des participants et leurs scores:
On ouvre le fichier "Resultats-NSI 1_re Collecter.csv.csv" par la fonction open() et on lit sa première ligne avec fichier.readline(). On va récupérer l'ensemble des noms des colonnes du tableurs excel avec la troisième ligne en prenant en compte que les éléments qui les sépares sont des ; avec ligne.strip().split(";"). On crée deux listes vides, Noms et scores. On va créer une boucle for pour le fichier ouvert. La liste elements va s'affecter l'ensemble des valeurs des colonnes. On va ajouter à la liste Noms, le quatrième élément de la liste elements qui est l'ensemble des prénoms des élèves. On va ajouter à la liste scores, le huitième élément de la liste elements qui est l'ensemble des notes des élèves. La dernière ligne ferme le fichier

Calcul des notes et fin du programme
Pour faire le calcul, on va créer une boucle for avec score élément de la liste scores, qui va s'appliquer pour tous les éléments de la liste scores. Dans celle-ci, on aura juste à affecter à une variable score, le calcul défini précédemment avec a et b pour trouver la note et l'ajouter à la liste vide note. La fonction round() permet d'arrondir le résultat en l'occurrence d'un chiffre après la virgule

Fin du programme

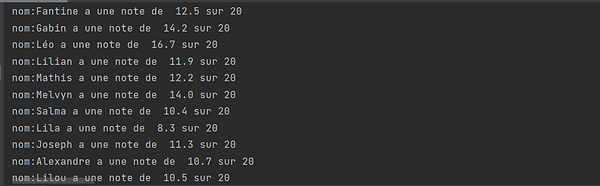
On crée une variable x=0 qui nous sera utile pour plus tard. On crée une boucle for() où i est un élément de l'ensemble Noms qui va afficher la chaîne de caractère"nom:", l'élément i qui va prendre toute les valeurs de Noms, une autre chaîne de caractère, l'élement x de la liste note qui est au début égal à zero et enfin une dernière chaîne de caractère.
À la fin de la boucle, on rajoute à x 1 pour qu'il nous donne la prochaine valeur de la liste note lors de l'affichage.




Projet du chapitre 2:Additionneur un bit
Faire sur python, un additionneur de deux nombres binaires en utilisant les expressions booléennes ET, OU, NON,... Pour nous aider, M.Laclaverie nous a déjà fait une partie du programme.
Additionner les nombres en binaire
L'addition des nombres binaires se fait de droite à gauche. Or, dans les listes, les nombres binaires sont du plus grand au plus petit. Pour additionner les deux nombres, il faut donc faire lire les listes de droite à gauche:
On voit que pour lire une liste dans l'autre sens, il y a une méthode particulière. En effet, dans les paramètres de la boucle, il faut indiquer le plus grand élément de la liste, ici 2, indiquer l'élément sur lequel on s'arrête, -1 et enfin, le pas de la boucle, -1 qui signifie que la liste est lu à reculons. Exactement ce qu'il nous faut pour lire de droite à gauche. De plus, pour additioner chaque valeur entre eux, les nombres seront contenus dans des listes n et p où chaque chiffre sera séparé pour l'addition.


Ajouter la dernière retenue
En effet, l'autre problème à résoudre était la dernière retenue car la boucle ne se répétant que le nombre des valeurs de la liste contenant un des termes de cette somme. Or, si la retenue était égale à 1, il fallait la rajouter au résultat car sinon la somme serait fausse. Pour résoudre ce problème, il fallut rajouter à la liste complète r(résultat) contenant la somme, la dernière retenue du calcul. Pour cela, il a fallut la faire hors de la boucle.
Le fonctionnement de la boucle
On va créer une boucle for () avec L'élément i qui va partir de 7 arriver à -1 avec un pas de -1.On crée un variable c qui sera la retenue. On affecte à la variable a l'élément n[i]. On affecte à la variable b l'élément p[i]. On affecte à la valeur unite les différentes possibilités de résultat. On ajoute à la liste r, la variable unite en nombre entier. On affecte à la variable c les différentes valeurs possibles de la retenue. Ainsi, on fait l'addition terme à terme des deux nombres binaires en prenant compte des retenues que l'on ajoute.


Les valeurs entre crochets sont l'addition binaire terme à terme avec le précédent qui est affiché à chaque fois, leurs affichages sont dues à print(r) dans la boucle. Les nombres hors crochets sont la valeur de la retenue de l'addition terme à terme, leurs affichages sont dues à print(c) dans la boucle. La valeur finale de r est le dernier groupe de valeurs
Projet du Chapitre 5:Tris
Faire un graphique montrant les temps que prennent des algorithmes de tri pour trier des listes de plus en plus longues
Le programme sera à créer sur python. La première liste sera de 1000 éléments et on multipliera dix fois 1000 par i pour créer de listes de longueur croissante. Le site contient l'explication en détail de trois tris où je n'ai pas eu de problème et deux tris où j'ai eu des problèmes.
Importation des modules
On va importer le module random pour intégrer des actions aléatoires. Il va nous servir à créer une liste de valeurs dans le désordre et la mélanger pour que l'ordinateur puisse la trier avec les différents tris. On importe la fonction * du module time pour accéder à l'horloge de l'ordinateur. On importe le module matplotlib.pyplot pour créer le graphique qui contiendra le temps de tri pour chaque liste. Enfin, on importe le module numpy pour créer les courbes de chaque tri.

Création de la liste
Avec la fonction creation_de_liste qui ne prend rien en paramètre, on va créer une liste de i*1000 éléments avec la boucle for() qui prendront une valeur aléatoire entre 1 et 100 avec random.randint().

Le tri sort
programme donné par le professeur
Dans cette fonction, on définit le tri sort(). On va chercher le temps que met le tri pour trier la liste avec les variables t3 et t4 à qui on affecte le temps interne de l'ordinateur. Puis, on soustrait ces deux temps pour avoir le temps que met l'ordinateur pour trier avec ce tri. On affecte cette différence à la variable duree1 que l'on ajoute à la liste resultats.sort. Enfin, on remélange la liste pour éviter que les autres tris aient une liste déjà triée ce qui fausserait les temps.
Je n'ai pas rencontré de difficultés particulières avec ce tri.

Le tri sorted
programme donné par le professeur
Dans cette fonction, on définit le tri sorted(). On va chercher le temps que met le tri pour trier la liste avec les variables t1 et t2 à qui on affecte le temps interne de l'ordinateur. Puis, on soustrait ces deux temps pour avoir le temps que met l'ordinateur pour trier avec ce tri. On affecte cette différence à la variable duree que l'on ajoute à la liste resultats.sorted.
Je n'ai pas rencontré de difficultés particulières avec ce tri.

Le tri à bulle
programme trouvé sur:
https://waytolearnx.com/2019/04/tri-a-bulle-en-python.html
le tri à bulle consiste à comparer deux éléments côte-à-côte de la liste et les intervertir si nécessaire. Il faut pour cela utiliser une case mémoire annexe.
On va définir la fonction tri_bulle qui va prendre liste en paramètre.
On affecte à la variable n la longueur du paramètre liste. On crée une boucle for qui prend en élément i qui va se répéter n fois. A l'intérieur, on crée une boucle for qui prend en élément j qui va partir de zero pour arriver à n-i-1, cela permettra de comparer l'ensemble des éléments.. On utilise la fonction if pour savoir si l'élément liste[j] est supérieur à l'élément liste[j+1]. Dans la dernière ligne de la fonction, on intervertit les deux éléments.
Pour clarifier, j'ai crée une fonction durre_tri_bulle qui prend en paramètre liste pour mesurer le temps avec la même méthode que sort() que prend le tri à bulle pour trier la liste, que j'ajoute ensuite à la liste resultats_bulle.
Je n'ai pas rencontré de difficultés particulières pour ce code.

Le tri par fusion
programme trouvé sur:
https://128mots.com/2019/12/03/le-tri-fusion-et-implementation-python-en-moins-de-128-mots/
Le tri par fusion consiste à trier des sous-listes de deux éléments, puis de les fusionner avec les sous-listes voisines jusqu'à ce que l'ensemble de la liste soit triée.
On crée une fonction tri_fusion() qui prend en paramètre tableau. On crée une boucle if pour savoir si tableau est composé d'un ou zéro éléments pour savoir si on doit trier tableau ou pas. On affecte à la variable pivot le quotient de la division euclidienne de la longueur de tableau par 2.
On affecte aux variables tableau1 et tableau2 une partie différente égale des éléments de tableau à qui ont soumet la fonction tri_fusion() en affectant les résultats aux variables gauche et droite. Puis, on applique la fonction fusion qui va prendre en paramètre gauche et droite.
Le programme de la fonction fusion est compliqué et je vais essayer de le résumer en quelques lignes. La première fonction while permet de comparer les éléments de tableau1 et tableau2 pour les ranger dans l'ordre croissant tant que la variable indice_tableau1 soit inférieur à taille_tableau1 et que la variable indice_tableau 2 soit inférieur à taille_tableau2. Les deux autres fonctions while, je ne l'est s'ai pas trop comprises.
J'ai rencontré des difficultés en essayant de calculer le temps que met le programme pour trier la liste.
Dans ce programme, j'ai mit le calcul du temps dans la fonction tri_fusion, ce qui m'a donné les temps qu'il a pris pour comparer toutes les éléments entre eux. Donc, je me suis retrouvé avec 11 éléments dans la liste resultats
. Ce qui pose problème car je ne veut que le temps du tri en entier, c'est pour cela que j'ai crée une fonction temps_fusion qui me permet d'avoir qu'un seul temps et le bon.




Le tri rapide
Le tri rapide consiste à "La méthode consiste à placer un élément du tableau (appelé pivot) à sa place définitive, en permutant tous les éléments de telle sorte que tous ceux qui sont inférieurs au pivot soient à sa gauche et que tous ceux qui sont supérieurs au pivot soient à sa droite. Cette opération s'appelle le partitionnement. Pour chacun des sous-tableaux, on définit un nouveau pivot et on répète l'opération de partitionnement. Ce processus est répété récursivement, jusqu'à ce que l'ensemble des éléments soit trié." Wikipédia, Tri rapide,https://fr.wikipedia.org/wiki/Tri_rapide.
Pour pouvoir tester l'efficacité du programme, je vais lui faire trier ma liste. Dans un premier temps, je crée une fonction tri_rapide qui va prendre liste en paramètre. La fonction if sert à éviter que le programme plante si la liste qui doit être triée est vide. Puis on affecte à liste_g et liste_d des listes vides. Ensuite on crée une boucle for qui se répètera par le nombre égal à la longueur de liste. Après, une fonction if sert à savoir si l'élément i de liste est inférieur ou égal à liste[0] donc l'élément 0 de liste devient le pivot car on ajoute liste[i] à soit liste_g ou liste_d. Enfin, on renvoie la liste_g et la liste_d à qui on applique la fonction tri_rapide où leur élément 0 deviendra pivot et la liste contenant liste[0] pour que l'ordinateur garde ces valeurs en mémoires avec la fonction return.
Difficultés rencontrées:
Comme pour le tri à fusion, j'ai eu un problème avec la récupération des temps. En effet, dans la première version, j'avais mis la récupération du temps dans la fonction tri_rapide:
En affichant la liste qui devait contenir le temps, elle était vide:
Donc pour régler le problème, j'ai crée une fonction duree_tri_rapide qui va mesurer le temps que prend le tri pour trier la liste.


Appels des fonctions.

Création du graphique
Pour tracer le graphique, on va créer une fonction tracer_figure qui va prendre en paramètre les listes que l'on a crée, plt.figsize sert à donner la taille du graphique. Pour tracer les points, on utilise plt.plot() où l'on met en premier la liste des abscisses, puis celle des ordonnées,"o" sert à enlever lest traits reliant la droite, marker à dire de quelle forme sera le point, color sa couleur et label de faire afficher dans la légende la correspondance entre le point et le tri. plt.xlabel et .ylabel() sert à donner un titre aux axes. plt.ttle, un titre au graphique. plt.legend() va servir à afficher la légende et plt.show à faire afficher l'ensemble du graphique. Enfin, on appelle la fonction pour faire un graphique avec les listes contenant les résultats de temps de triage pour chaque tris.

Tracer les courbes
programme donné par le professeur
Pour cela, je crée une fonction modele qui va prendre liste en paramètre. On va affecter à la variable x, np.array() avec une liste à l'intérieur qui va où l'élément i va prendre les valeurs entre 1000 et 11000 avec un pas de 1000. On affecte à la variable y np.array() avec liste. On affecte à la variable modele la fonction np.polyfit() qui permet d'obtenir les paramètres de la fonction polynomiales, elle va prendre x, y et 2 en paramètre. On affecte à la variable xm la fonction np.linspace() qui va permettre de tracer un tableau en une dimension avec en paramètre 1000,11000 et 1000. On affecte à la variable ym la fonction polynomiales. Enfin, on affiche la courbe de la fonction avec un label où la fonction est indiquée.

programme en entier:






Résultats



Hypothèse et Conclusion
Dans un premier temps, on remarque que le temps augmente que prend chaque tris pour trier quand le nombre d'éléments à trier augmente, ce qui est tout à fait logique. Cependant, on remarque que certains tris sont plus rapide que d'autres, les tris sort(), sorted(), rapide* et par fusion** sont les plus rapides avec chaque fois un temps proche de zéro. Tandis que les tris par insertion*** et sélection**** sont plus lents. Enfin, le tri le plus lent est le tri à bulle*****. Cette hypothèse est renforcée par les courbes de tendance, en effet, les fonctions prédisant les temps de tris en fonction du nombre d'éléments sont pour les tris les plus rapides(sort(), sorted(), rapide et par fusion) de simples fonctions linéaires avec un coefficient directeur minuscules, exemple:2,26E-6, ce qui nous donne l'impression que le tri se fait de manière instantanée. Pour les tris par sélection et sélection, qui ont des courbes qui sont proches, les fonctions sont des polynômes du second degré avec des a à E-8 et des b négatifs. Cependant, le changement est que l'on a maintenant un x² se qui augmente les résultats par rapport aux tris ayant une fonction linéaire. Le dernier, le tris à bulle a quant à lui une fonction du second degré avec a=1,63E-7 ce qui va donner des résultats un peu plus grand. Ainsi, le tri à bulle est le plus lent que tous les autres tris, cela est logique avec son tri qui prend trop de temps car il compare que deux éléments à chaque fois et doit se répéter n fois avec n-i-1 qui est égal aux nombres d'élément de la liste moins i qui est l'élément de la première boucle et qui va prendre l'ensemble des valeurs entre 0 et n exclu dans la liste en plus de se répéter n fois déjà dans la première boucle. Ensuite viennent le tri par sélection et insertion, les deux tris ayant souvent des temps similaires, le tri par insertion va certes se répéter n de fois comme le tri à bulle, la différence étant la boucle while qui va donc moins se répéter que la deuxième boucle for(), de plus cela est logique car le tri par insertion ne compare pas l'élément suivant juste avec le précédent, il le compare avec l'ensemble des éléments précédent se qui lui évite de devoir retester la liste car elle est entièrement triée après qu'il a comparer tous les éléments une première fois. . Le tri par sélection, lui, fonctionne en sélectionnant le minimum de la liste, le place au début et cherche le minimum de la liste restante pour aller le placer après le premier minimum et ainsi de suite. Il fait donc n-1 comparaisons.Il sera moins long que le tri à bulle car même si il est composé de deux boucles for(), il va comparer tous les éléments d'un coup pour trouver le minimum(deuxième boucle) et va répéter cette action n-1 fois(première boucle). Cependant, il reste toujours un peu plus lent que le tri par insertion. Pour les tris les plus rapides, le tri par fusion quant à lui par son fonctionnement reposant sur l'observation demande moins de temps. En effet, l'idée du tri est de trier une liste en la divisant en petites listes que l'on compare entre elles, cela rend donc la comparaison rapide car les comparaisons sont moins longues, très facile et efficace sur les grandes listes. Les tris sort() et sorted() sont aussi très rapides ce qui est logique car se sont les algorithmes de tris naturellement implantées dans Python. Enfin, le tri rapide porte bien son nom car même si il est théoriquement non stable, il est l'un des plus rapide et est couramment utilisé. Il va utiliser une technique mélangeant le tri à bulle et le tri par sélection, en effet, il va comparer deux éléments mais pas forcément collés l'un à l'autre et les intervertir s'il y a besoin. Cela le rend très rapide car il n'a besoin que d'une boucle for().
En conclusion, pour les listes de moins de milles éléments on peut utiliser tous les tris, cependant, qu'en on augmente le nombre d'élément, il est préférable d'utiliser le tri rapide, sort(), sorted() ou par fusion pour gaspiller le moins de temps possible.
Projet: prévoir la survie d'un passager sur le Titanic.
"Le RMS Titanic est un paquebot transatlantique britannique qui fait naufrage dans l'océan Atlantique Nord en 1912 à la suite d'une collision avec un iceberg, lors de son voyage inaugural de Southampton à New York. Entre 1 490 et 1 520 personnes trouvent la mort, ce qui fait de cet événement l'une des plus grandes catastrophes maritimes survenues en temps de paix et la plus grande pour l'époque."
Wikipedia,https://fr.wikipedia.org/wiki/Titanic
Le but du projet est de savoir si des caractéristiques telles que le sexe, laclasse ou encore l'âge ont joués sur le poucentage de chance de survie d'un ou une passager(ère). Pour cela, nous avons à notre disposition, un document excel contenant l'âge, le nombre de parents ou d'enfants, la classe, le sexe, le nombre de frères ou de conjoints, le prix du billet.
Utilisation des données.
On va utiliser le programme ci-dessous pour pouvoir exprimer le nombre de personnes mortes ou en vies pour chaque catégorie.



Parch(Nombre de Parents ou d'enfants):
On voit dans ce diagramme que les passagers n'ayant pas d'enfants ou de parents ont un nombre de morts supérieur à 400 pour un nombre de survivants arrivant à environ 240. Tandis que les passagers ayant 1 ou 2 parents ou enfants à bord sont certes moins nombreux mais en terme de pourcentage, il y avait plus de chances de survie si l'on avait 1 ou 2 parents ou enfants à bord.
Pclass(classe du passager):
On voit dans ce diagramme que les passagers de première classe ont en majorité survécu(140 survivants/70 morts). Pour la 2eme classe, même si le nombre de morts est plus élevés que le nombre de morts, les différences sont assez faibles(100 morts/90 survivants). Par contre, les passagers de la 3eme classe, les plus pauvres sont en majorités morts dans l'incident et de loin(360 morts/140 survivants). Ce diagramme est fondamental car il montre l'inégalité des chances de survie des passagers par rapport à la richesse, les 1ere classes étant les plus riches.
SibSp(nombre de frères, de sœurs et de conjoint):
Ce graphique représente le nombre de survivants et de morts en fonction du nombre de conjoints et de frères ou de sœurs . On voit que en terme de pourcentage, il y eu plus de survivants avec 1 ou 2 conjoints ou frères et sœurs.

Age(age du passager):
Dans ce graphique, on voit le nombre de survivants et le nombre de morts par rapport à l'âge. On remarque que en terme de statistiques que les enfants et adolescents(0-20 ans) ont eu de meilleures chances de survies que les jeunes adultes(20-30 ans). De plus, les personnes âgées (60-80 ans) ont eu des chances diverses, il y eu autant de survivants que de morts chez les 80 ans, que des victimes chez les 70 ans et 1/3 de survivants chez les 60 ans.

Sexe(sexe du passager):
Ce graphique montre le nombre de survivants et de victimes en fonction du sexe, 0 représentant le sexe féminin et 1 le sexe masculin. On peut en déduire que les femmes ont eu des meilleures chances de survie que les hommes.

Fare(prix du billet du passager):
Ce graphique montre le nombre de survivants et de morts, en fonction du billets. Comme le graphique du nombre de morts et de survivants en fonction de la classe, celui-ci montre bien les plus riches ont eu plus de chances de survies que les plus pauvres car les tickets les moins chers ont été acheté par les personnes pauvres qui sont mortes pour le 2/3 d'entre elles et inversement pour les plus riches.



Conclusion
Le programme affiche tout le temps que le personnage meure même avec les caractéristiques optimales pour la survie sur le Titanic. On peut donc conclure que nôtre programme n'est pas suffisamment poussée pour faire ce genre de programme.

